Module 1 - Part 1: Deafness / Hearing Example

[M1.P1.Example-1: Hearing Example] Consider the following case study centered on potential insurance fraud regarding deafness. This case study was presented in an article by Pankratz, Fausti, and Peed titled “A Forced-Choice Technique to Evaluate Deafness in the Hysterical or Malingering Patient.” The following is an excerpt from the article.
Source: Journal of Consulting and Clinical Psychology, 1975, Vol. 43, pg. 421-422.
The patient was a 27-year-old male with a history of multiple hospitalizations for idiopathic convulsive disorder, functional disabilities, accidents, and personality problems. His hospital records indicated that he was manipulative, exaggerated his symptoms to his advantage, and that he was a generally disruptive patient. He made repeated attempts to obtain compensation for his disabilities. During his present hospitalization he complained of bilateral hearing loss, left-sided weakness, left-sided numbness, intermittent speech difficulty, and memory deficit. There were few consistent or objective findings for these complaints. All of his symptoms disappeared quickly with the exception of the alleged hearing loss.
| To assess his alleged hearing loss, testing was conducted through earphones with the subject seated in a sound-treated audiology testing chamber. Visual stimuli utilized during the investigation were produced by a red and a blue light bulb, which were mounted behind a one-way mirror so that the subject could see the bulbs only when they were illuminated by the examiner. The subject was presented several trials on each of which the red and then the blue light were turned on consecutively for 2 seconds each. On each trial, a 1,000-Hz tone was randomly paired with the illumination of either the blue or red light bulb, and the subject was instructed to indicate with which light bulb the tone was paired. Because the researchers were implementing a “forced-choice” technique, the subject was forced to answer each time with either ‘red’ or ‘blue’. |
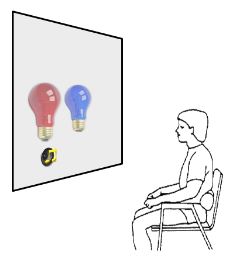
|
Hearing Simulation App: Link
Understanding Outcomes
Suppose an individual was asked to participate in the hearing evaluation experiment presented above. A total of 20 trials of the experiment were conducted.
| Situation A | Outcome | Number |
| Number of times an individual was able to correctly associate the light with the playing of the sound | 20 | |
| Number incorrect | 0 | |
| Total | 20 |
| Situation B | Outcome | Number |
| Number of times an individual was able to correctly associate the light with the playing of the sound | 10 | |
| Number incorrect | 10 | |
| Total | 20 |
Questions
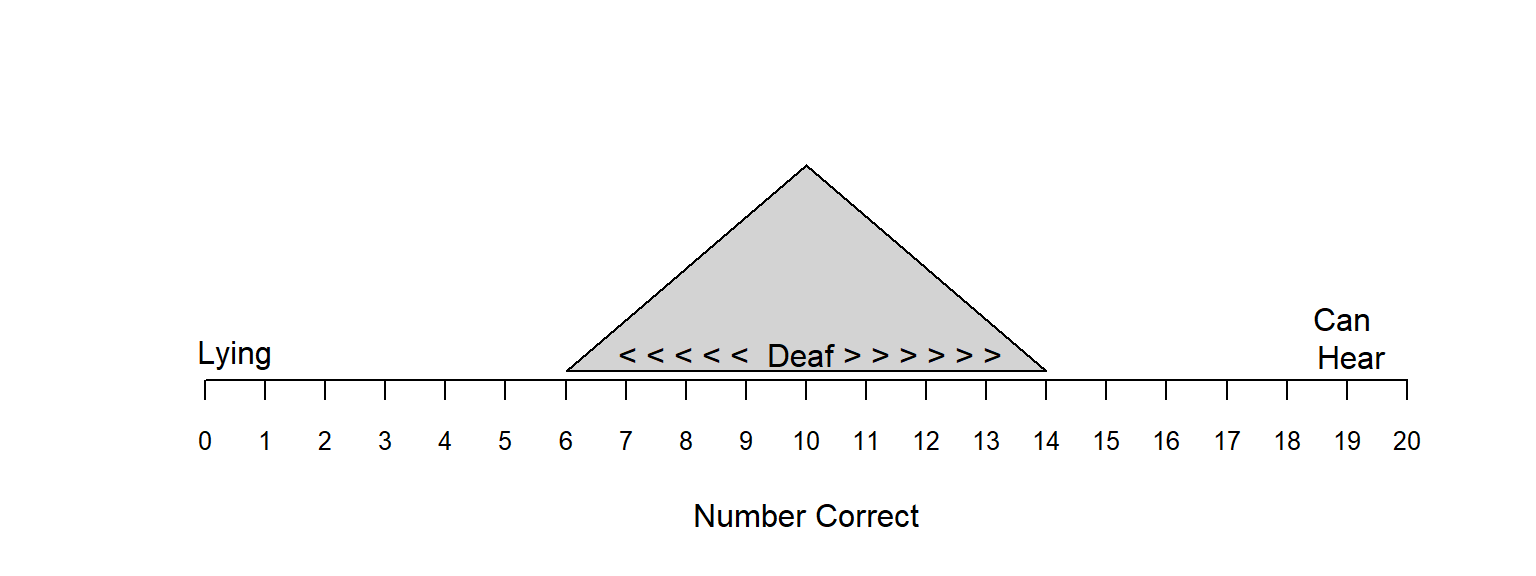
Next, let us consider a third situation.
| Situation C | Outcome | Number |
| Number of times an individual was able to correctly associate the light with the playing of the sound | 0 | |
| Number incorrect | 20 | |
| Total | 20 |
Question
Statistical methods can be used to help fight against insurance fraud. In this situation, it is necessary to determine whether or not the subject in this investigation is intentionally giving the wrong answers. In order to make a determination of this nature, we must first gain an understanding of likely versus unlikely outcomes. A simulation model can be used to identify likely outcomes given a particular situation.
Modeling Deaf Outcomes
A simulation model will be constructed to mimic the outcomes of a deaf person. This model requires the identification of two pieces of information.
- Number of completed trials
- The likelihood or chance of obtaining a correct response
For our example, the number of completed trials is 20, and the chance of obtaining a correct response for a deaf person is 1 out of 2, or 50%.
| Necessary Information for Building a Statistical Model | Values |
| Number of completed trials | 20 |
| The likelihood or chance of a corrrect response | 1 out of 2; i.e. \(\frac{1}{2}\) |
The expected outcome for the number of correct responses for 20 trials with each trial having a 1/2 chance of being correct is 10.
\[ Expected \space Value = 20 * \frac{1}{2} = 10 \]
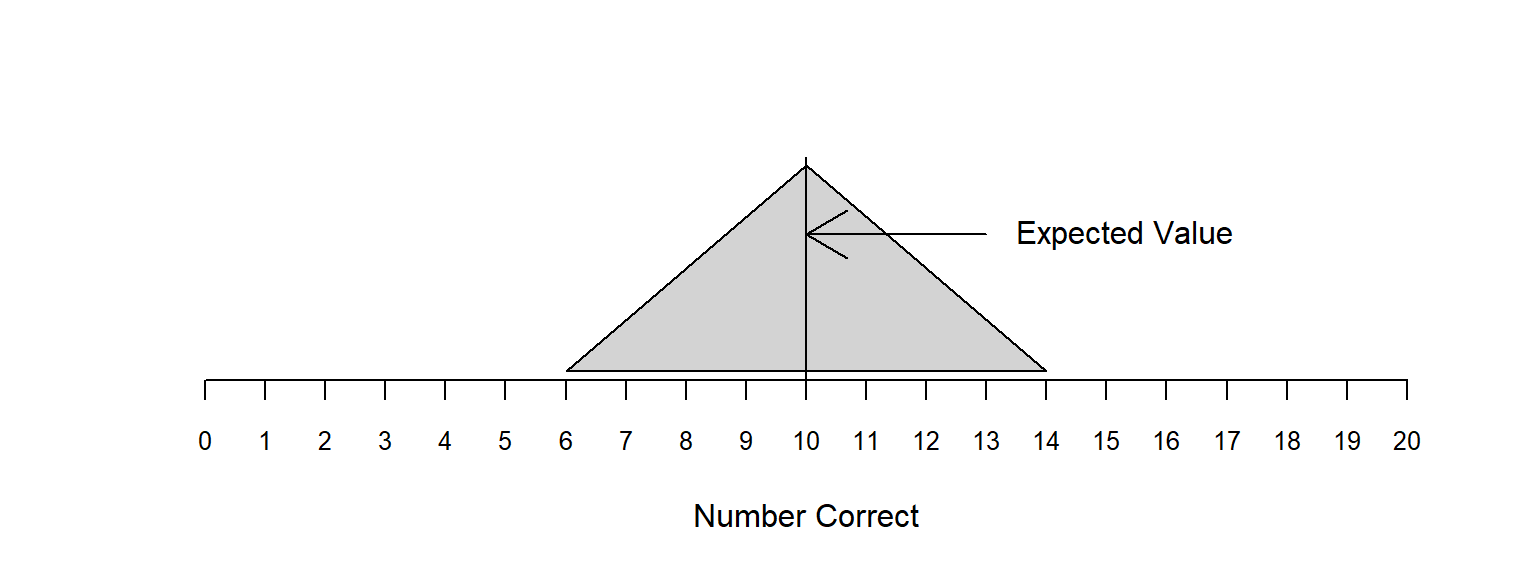
| Definition |
| The expected outcome is the outcome which is identified as the most likley outcome. |
The expected value for the model presented here with a \(\frac{1}{2}\) chance of being correct will be in the middle; i.e., halfway across the number line representing the number correct.
The most important element that a statistical approach provides to solving a problem of this nature is an understanding of the inherent variation that exists in the outcomes from the model. In particular, there is inherent variation (i.e., randomness) present in the number of correct responses over repeated trials. The amount of inherent variation depends on the model being used. In this situation, the number of trials and the likelihood of a correct response determine the amount of inherent variation.
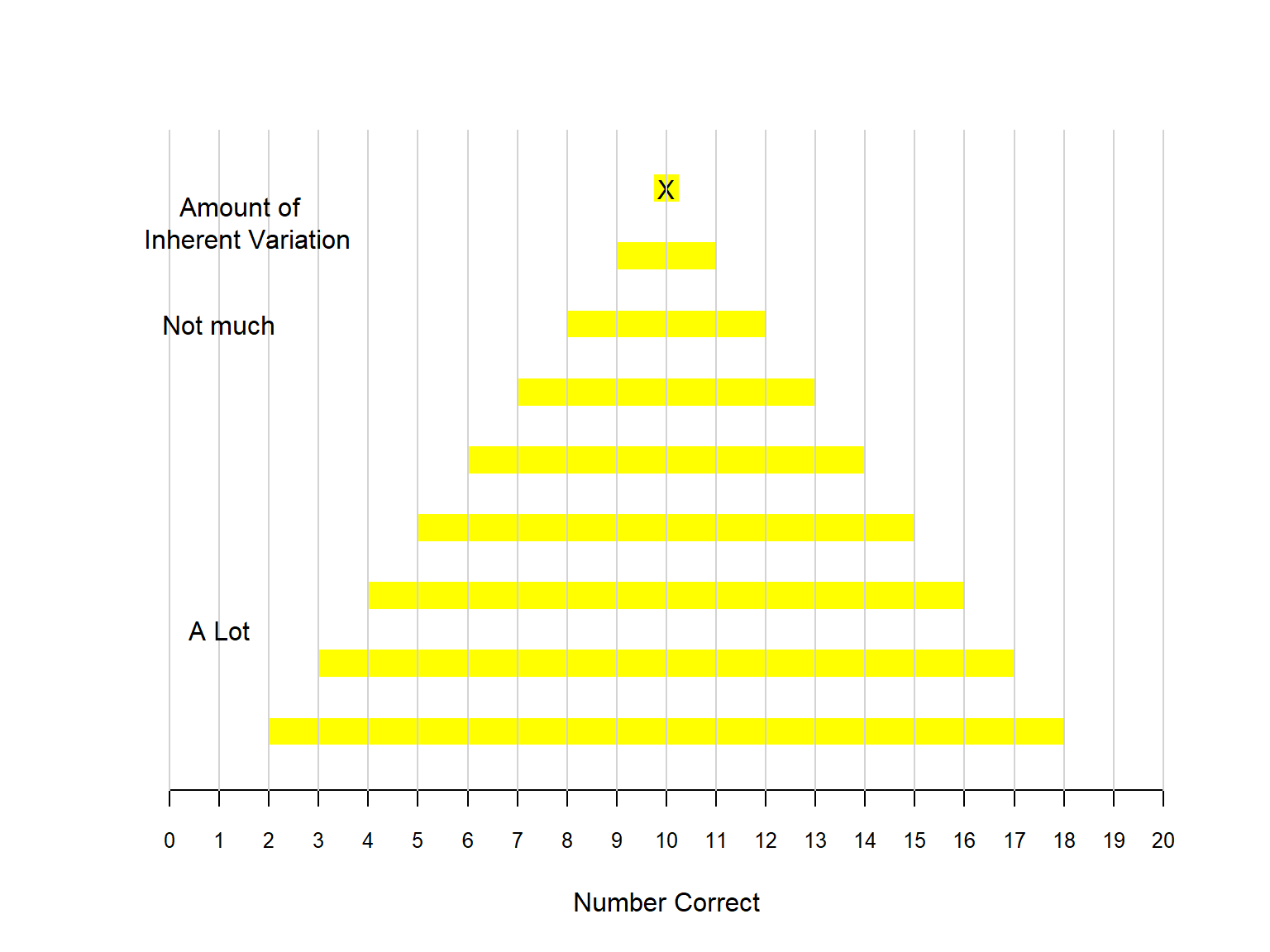
The amount of inherent variation can be measured using either simulaiton models or mathematical formulas. A variety of software technologies have been developed to construct simulation models, and some type of random device is a necessary part of their development. For the simple type provided here, a fair coin is sufficient for determining the amount of inherent variation in the outcomes of interest because the likelihood of a correct response is \(\frac{1}{2}\).